Algoritma Prim

Dalam tutorial ini, anda akan belajar bagaimana Algoritma Prim berfungsi. Anda juga akan mendapat contoh Algoritma Prim di C, C ++, Java dan Python.

Algoritma Prim adalah algoritma pokok rentang minimum yang mengambil graf sebagai input dan mencari subset tepi graf itu yang

membentuk pokok yang merangkumi setiap bucu
mempunyai jumlah bobot minimum di antara semua pokok yang boleh terbentuk dari graf

Bagaimana algoritma Prim berfungsi

Ia berada di bawah kelas algoritma yang disebut rakus rakus yang mencari optimum tempatan dengan harapan dapat mencari optimum global.

Kami bermula dari satu bucu dan terus menambah tepi dengan berat paling rendah sehingga kami mencapai matlamat kami.

Langkah-langkah untuk melaksanakan algoritma Prim adalah seperti berikut:

Memulakan pokok rentang minimum dengan bucu yang dipilih secara rawak.
Cari semua tepi yang menghubungkan pokok ke bucu baru, cari minimum dan tambahkan ke pokok
Terus ulangi langkah 2 sehingga kami mendapat pokok minimum

Contoh algoritma Prim

Mulakan dengan graf berwajaran

Pilih bucu

Pilih pinggir terpendek dari bucu ini dan tambahkannya

Pilih bucu terdekat yang belum ada dalam penyelesaian

Pilih pinggir terdekat yang belum ada dalam penyelesaiannya, jika terdapat banyak pilihan, pilih satu secara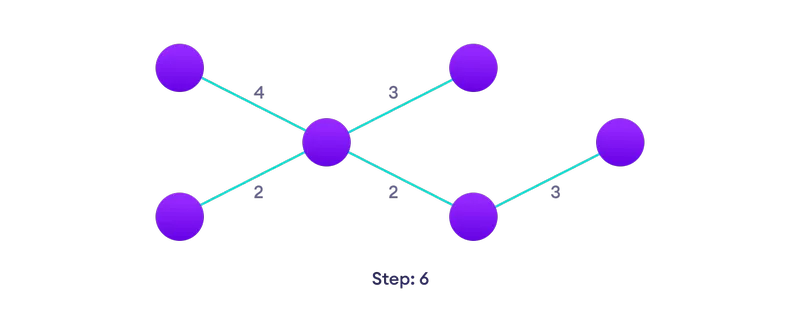

berulang-ulang sehingga anda mempunyai pokok rentang

Pseudokod Algoritma Prim

Algoritma pseudocode untuk prim menunjukkan bagaimana kita membuat dua set titik U dan VU. U mengandungi senarai bucu yang telah dikunjungi dan VU senarai bucu yang belum. Satu demi satu, kami memindahkan bucu dari set VU ke set U dengan menghubungkan tepi dengan berat paling sedikit.

 T = ∅; U = ( 1 ); while (U ≠ V) let (u, v) be the lowest cost edge such that u ∈ U and v ∈ V - U; T = T ∪ ((u, v)) U = U ∪ (v)

Contoh Python, Java dan C / C ++

Walaupun representasi grafik matriks adjacency digunakan, algoritma ini juga dapat dilaksanakan dengan menggunakan Adjacency List untuk meningkatkan kecekapannya.

Python Java C C ++

 # Prim's Algorithm in Python INF = 9999999 # number of vertices in graph V = 5 # create a 2d array of size 5x5 # for adjacency matrix to represent graph G = ((0, 9, 75, 0, 0), (9, 0, 95, 19, 42), (75, 95, 0, 51, 66), (0, 19, 51, 0, 31), (0, 42, 66, 31, 0)) # create a array to track selected vertex # selected will become true otherwise false selected = (0, 0, 0, 0, 0) # set number of edge to 0 no_edge = 0 # the number of egde in minimum spanning tree will be # always less than(V - 1), where V is number of vertices in # graph # choose 0th vertex and make it true selected(0) = True # print for edge and weight print("Edge : Weight") while (no_edge  G(i)(j): minimum = G(i)(j) x = i y = j print(str(x) + "-" + str(y) + ":" + str(G(x)(y))) selected(y) = True no_edge += 1

 // Prim's Algorithm in Java import java.util.Arrays; class PGraph ( public void Prim(int G()(), int V) ( int INF = 9999999; int no_edge; // number of edge // create a array to track selected vertex // selected will become true otherwise false boolean() selected = new boolean(V); // set selected false initially Arrays.fill(selected, false); // set number of edge to 0 no_edge = 0; // the number of egde in minimum spanning tree will be // always less than (V -1), where V is number of vertices in // graph // choose 0th vertex and make it true selected(0) = true; // print for edge and weight System.out.println("Edge : Weight"); while (no_edge < V - 1) ( // For every vertex in the set S, find the all adjacent vertices // , calculate the distance from the vertex selected at step 1. // if the vertex is already in the set S, discard it otherwise // choose another vertex nearest to selected vertex at step 1. int min = INF; int x = 0; // row number int y = 0; // col number for (int i = 0; i < V; i++) ( if (selected(i) == true) ( for (int j = 0; j G(i)(j)) ( min = G(i)(j); x = i; y = j; ) ) ) ) ) System.out.println(x + " - " + y + " : " + G(x)(y)); selected(y) = true; no_edge++; ) ) public static void main(String() args) ( PGraph g = new PGraph(); // number of vertices in grapj int V = 5; // create a 2d array of size 5x5 // for adjacency matrix to represent graph int()() G = ( ( 0, 9, 75, 0, 0 ), ( 9, 0, 95, 19, 42 ), ( 75, 95, 0, 51, 66 ), ( 0, 19, 51, 0, 31 ), ( 0, 42, 66, 31, 0 ) ); g.Prim(G, V); ) )

 // Prim's Algorithm in C #include #include #define INF 9999999 // number of vertices in graph #define V 5 // create a 2d array of size 5x5 //for adjacency matrix to represent graph int G(V)(V) = ( (0, 9, 75, 0, 0), (9, 0, 95, 19, 42), (75, 95, 0, 51, 66), (0, 19, 51, 0, 31), (0, 42, 66, 31, 0)); int main() ( int no_edge; // number of edge // create a array to track selected vertex // selected will become true otherwise false int selected(V); // set selected false initially memset(selected, false, sizeof(selected)); // set number of edge to 0 no_edge = 0; // the number of egde in minimum spanning tree will be // always less than (V -1), where V is number of vertices in //graph // choose 0th vertex and make it true selected(0) = true; int x; // row number int y; // col number // print for edge and weight printf("Edge : Weight"); while (no_edge < V - 1) ( //For every vertex in the set S, find the all adjacent vertices // , calculate the distance from the vertex selected at step 1. // if the vertex is already in the set S, discard it otherwise //choose another vertex nearest to selected vertex at step 1. int min = INF; x = 0; y = 0; for (int i = 0; i < V; i++) ( if (selected(i)) ( for (int j = 0; j G(i)(j)) ( min = G(i)(j); x = i; y = j; ) ) ) ) ) printf("%d - %d : %d", x, y, G(x)(y)); selected(y) = true; no_edge++; ) return 0; )

 // Prim's Algorithm in C++ #include #include using namespace std; #define INF 9999999 // number of vertices in grapj #define V 5 // create a 2d array of size 5x5 //for adjacency matrix to represent graph int G(V)(V) = ( (0, 9, 75, 0, 0), (9, 0, 95, 19, 42), (75, 95, 0, 51, 66), (0, 19, 51, 0, 31), (0, 42, 66, 31, 0)); int main() ( int no_edge; // number of edge // create a array to track selected vertex // selected will become true otherwise false int selected(V); // set selected false initially memset(selected, false, sizeof(selected)); // set number of edge to 0 no_edge = 0; // the number of egde in minimum spanning tree will be // always less than (V -1), where V is number of vertices in //graph // choose 0th vertex and make it true selected(0) = true; int x; // row number int y; // col number // print for edge and weight cout << "Edge" << " : " << "Weight"; cout << endl; while (no_edge < V - 1) ( //For every vertex in the set S, find the all adjacent vertices // , calculate the distance from the vertex selected at step 1. // if the vertex is already in the set S, discard it otherwise //choose another vertex nearest to selected vertex at step 1. int min = INF; x = 0; y = 0; for (int i = 0; i < V; i++) ( if (selected(i)) ( for (int j = 0; j G(i)(j)) ( min = G(i)(j); x = i; y = j; ) ) ) ) ) cout << x << " - " << y << " : " << G(x)(y); cout << endl; selected(y) = true; no_edge++; ) return 0; )

Algoritma Prim vs Kruskal

Algoritma Kruskal adalah algoritma pokok rentang minimum yang popular yang menggunakan logik yang berbeza untuk mencari MST graf. Daripada bermula dari bucu, algoritma Kruskal menyusun semua tepi dari berat rendah ke tinggi dan terus menambahkan tepi paling rendah, mengabaikan tepi yang membuat kitaran.